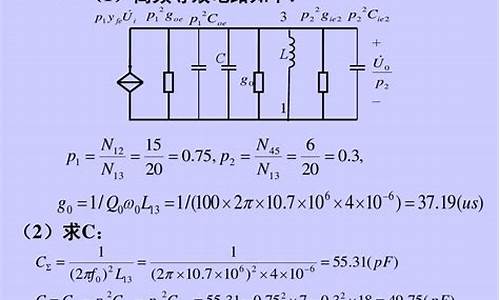
高频电子线路是现代电子技术中的重要组成部分,其应用范围广泛,包括通信、雷达、医疗等领域。在高频电子线路的设计和分析中,数学知识点起着至关重要的作用。本文将介绍高频电子线路相关的数学知识点。
一、傅里叶变换与频域分析
傅里叶变换是研究信号在频域上变化规律的数学工具。在高频电子线路中,傅里叶变换被广泛应用于滤波器设计、调制解调器设计等方面。通过对信号进行傅里叶变换,可以将时域上的信号转换为频域上的信号,从而更好地分析和处理信号。
二、拉普拉斯变换与电路分析
拉普拉斯变换是一种将微分方程转化为代数方程的方法,可以用于电路分析。在高频电子线路中,拉普拉斯变换被广泛应用于电路稳定性分析、响应速度分析等方面。通过对电路进行拉普拉斯变换,可以更好地理解电路的特性和行为。
三、Z变换与系统稳定分析
Z变换是一种将离散时间系统转化为连续时间系统的数学工具,可以用于系统稳定分析。在高频电子线路中,Z变换被广泛应用于滤波器设计、放大器设计等方面。通过对系统进行Z变换,可以更好地分析系统的稳定性和性能。
四、小波变换与信号处理
小波变换是一种将时域或频域信号转换为另一种时域或频域信号的数学方法,可以用于信号处理。在高频电子线路中,小波变换被广泛应用于滤波器设计、去噪处理等方面。通过对信号进行小波变换,可以更好地提取信号的特征和信息。
五、复变函数与电路设计
复变函数是研究复数函数及其性质的数学工具,可以用于电路设计。在高频电子线路中,复变函数被广泛应用于滤波器设计、放大器设计等方面。通过对电路进行复变函数分析,可以更好地理解电路的特性和行为。
高频电子线路相关的数学知识点是其设计和分析的基础,掌握这些知识点可以帮助工程师更好地理解和处理高频电子线路中的复杂问题。
版权声明
本文仅代表作者观点,不代表百度立场。
本文系作者授权百度百家发表,未经许可,不得转载。











发表评论